One of the simpliest examples of dybamic programming in computer science in when you have to calculate the nth number in a fibonacci sequence. The way dynamic programming improves the straightforward naiive approach, is instead of calculating the fibonacci sequence for the numbers leading up to the nth number, we store the values in a map thereby removing all the uncessary recomputations that add the the time of the naiive algorithm approach. By removing uncessary operations we get to the most optimized version of the solving the ficonacci problem(the difference in time is from O(n^2) -> O(n)).

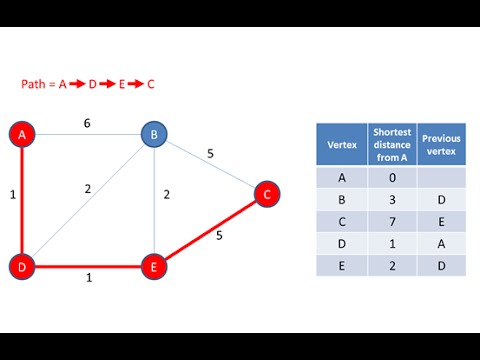
Another example dynamic programming is used is in path finding algorithms specifically Dijkstra's algorithm. There is a dynamic programming functional equation that this algorithm successively approximates the shortest distance from one node to another node. The algorithm starts with a beginning vertex and find the shortest paths to all other nodes in the graph. Here is a simple example of the algorithm: